مظاہر فطرت اور ریاضی کے اسرار

قدیم دور میں جب انسان میں شعور و تجسس کی حس نے کروٹ لینی شروع کی اور وہ اپنے اردگرد رونما ہونے والے قدرتی تغیرات و حالات کا بہ غور جائزہ لینے لگا، اُس وقت اس دنیا کی ہیئت موجودہ دور سے بےحد مختلف تھی۔ اُس وقت انسان نے اندازہ کیا کہ کائنات میں رونما ہونے والے کچھ واقعات باقاعدہ اور کچھ بے ضابطہ ہیں۔ 

مثلاً دن اور رات کا آنا جانا، موسموں کا بدلنا، چاند کی مختلف اشکال اور ستاروں سمیت دیگر اجرام فلکی کی حرکات وغیرہ ایک ترتیب سے گامزن ہیں جب کہ اچانک واقع ہونے والے بعض حالات و واقعات بظاہر بےقاعدہ اور اتفاقی ہیں۔ ریاضی بذات خود ایک ایسا جامع اور منفرد مضمون ہے، جس نے پوری سائنس اور بقیہ تمام علوم کو اپنی دسترس میں لے رکھاہے۔ 

غور کیا جائے تو پتہ چلےگا کہ ریاضی کی اپنی حیثیت کسی مضمون کی نہیں ہے بلکہ یہ دوسرے مضامین کے نظریات کےلیے ٹھوس ثبوت فراہم کرتا ہے، اسی وجہ سے ریاضی کو عموماً دو بڑے حصوں میں تقسیم کیا جاتا ہے، اول خالص ریاضی اور دوئم کو اطلاقی ریاضی کہتے ہیں۔ مضمون کی طوالت کے پیش نظر ان کی تفصیل ممکن نہیں، غرض کہ ریاضی ایسا مضمون ہے، جس کی مدد سے طبیعیات، کیمیاء، فلکیات اور سائنس کی دیگر شاخوں سے وابستہ نظریات کو درست تسلیم کرلیا جاتا ہے یا پھر غلط ثابت ہونے پر مسترد کردیا جاتا ہے۔چناں چہ ہم کہہ سکتے ہیں کہ انسانی دماغ بھی جب کوئی نظریہ،کوئی خیال، کوئی بات سوچتا ہے تو اسے ریاضی پر صحیح یا غلط ثابت کیا جاسکتا ہے۔ لارڈکیلون نے ایک مرتبہ کہا تھا کہ’’ اگر تم کسی چیز کی پیمائش نہیں کرسکتے ہو تو تم اس چیز کے بارے میں کچھ بھی نہیں جان سکتے۔‘‘

ارتقائے انسانی کے نقطہ آغاز سے ریاضی جنم لے چکی تھی کم از کم انسان چیزوں کی تعداد اور ان کی مقدار میں فرق محسوس کرسکتا تھا، اور جب اس نے اپنے خیالات کےلیے’’لفظ‘‘ ایجاد کیاتو دراصل ان خیالات کے پس منظر میں وہ ریاضی کے ہی اصولوں کی تشکیل کررہا تھا، جس طرح قدیم انسان نے ستاروں اور سیاروں سے کوئی نہ کوئی کہانی منسوب کررکھی تھی اسی طرح ریاضی میں بھی قدیم یونانیوں کا خیال تھا کہ جفت اعداد مونث ہوتے ہیں جو تقسیم ہوجاتے ہیں اور بکھر جاتے ہیں جب کہ طاق اعداد مذکر ہوتے ہیں جو کبھی تقسیم نہیں ہوتے اور ان میں آسمانی خصوصیات ہوتی ہیں۔ 

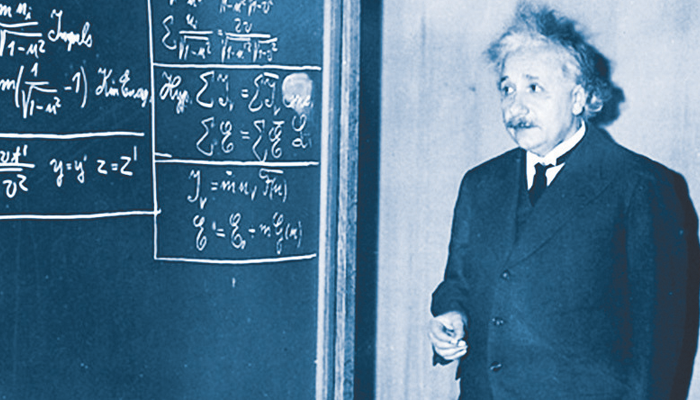
شروع ہی سے انسان کا ریاضی سے بڑا فطری تعلق رہاہے۔اسی وجہ سے اس نے تمام مظاہرفطرت کی تشریح ریاضیاتی طور پر ہی کی مثلاً سردی اور گرمی کوئی متضاد احساسات نہیں بلکہ سردی یعنی کم درجۂ حرارت اور گرمی یعنی زیادہ درجۂ حرارت دونوں ہی درجہ ٔحرارت کے درمیانی فرق کو واضح کرتے ہیں۔ یعنی سردی اور گرمی کی اپنی کوئی حیثیت نہیں بلکہ محض ایک پیمائش ہے اور پھر اسی پیمائش کو ہندسوں میں ظاہر کرکے تھرمامیٹر کا نام دے دیا گیا۔

زمان و مکان کےایک جزو زمان یعنی وقت کی جزئیات پر غور کریں تو معلوم ہوگا کہ وقت کا کہیں وجود نہیں لیکن پھر بھی دن اور رات کے پھیرے ’’وقت‘‘ کا احساس دلا تے ہیں۔ کیا وقت اسے کہتے ہیں کہ یہ زمین سورج کے گرد گھوم رہی ہے اور دوسرے ستارے و سیارے اور دیگر اجرام فلکی بھی محو گردش ہیں۔ جن کی مسلسل و مقررہ حرکت سے وقت پیدا ہوکر لامتناہی راستے پر سفر کررہاہے۔ اس نظریے کو درست مانتے ہوئے تھوڑی دیر کے لئے یہ فرض کرلیں کہ اس کائنات بشمول ہماری زمین تمام اجرام فلکیات بالکل ساکن حالحالت میں آجاتے ہیں تو پھر اُس وقت ’’وقت ‘‘ کی کیا اہمیت ہوگی؟ کیا مقام ہوگا؟ 

وقت صفر ہوجائے گا یعنی 0=T آئن اسٹائن نے اپنے نظریہ اضافیت میں ’’ٹائم ڈائیلیشن‘‘ (Time Dilation) کے ذریعے اسی نقطے کی وضاحت کی ہے کہ ایک جسم کی رفتار جس قدر تیز ہوتی جائے گی،وقت اس کےلیے سکڑتا جائے گا حتی کے وقت صفر ہوجائے اور اس وقت مادّہ مکمل طور پر توانائی میں تبدیل ہوچکا ہوگا۔ یعنی E=mc 2 لیکن بہرحال انسان نے دن اور رات کو بانس کے سائے، مٹکے میں گری ہوئی ریت اور گھڑیوں میں قید کرنے کی سعی لاحاصل کی۔ وہ اس لئے کہ انسان جس نظریہ سے مانوس ہوگیا تھا۔

آئن اسٹائن نے انسان کے اسی قدیم نظریہ وقت پر کاری ضرب لگائی اور اپنے نظریہ کو مکمل ریاضیاتی طور پر درست ثابت کردیا،جس طرح انسان نے وقت کی پیمائش کرنی شروع کردی اور اسے ہندسوں کے حوالے کردیا اسی طرح فاصلوں کو بھی ہندسوں سے ظاہر کیا جانے لگا لیکن کیا ہم نے کبھی یہ بات سوچی ہے کہ ہم وقت اور فاصلے کی پیمائش ہندسوں ہی سے کیوں کرتے ہیں؟ کیا اس کا کوئی دوسرا بھی طریقہ کار ہے؟ 

اگر گہرائی سےاس پر غور کریں تو ہمیں ریاضی کی صداقت پر یقین ہوجائے گا کہ درحقیقت اس وقت ریاضی اپنی جس شکل میں موجود ہے اسے ہم ’’الہامی‘‘ کہہ سکتے ہیں۔ جان نیپئر نے بھی دس کے عدد کو اساس بناکر لوگارتھم کا آغاز کیا۔ کائنات کے بڑے بڑے فاصلوں کو ناپنے کے لیئے لوگارتھم کو استعمال کیاجاتا ہے بلکہ نیپئر نے لوگارتھم ایجاد ہی اسی غرض سے کی تھی کہ وہ خود بھی علم فلکیات سے گہرا شغف رکھتا تھا۔ ریاضی دنیا کا سب سےقدیم اور جدید علم ہے۔ قدیم انسان نے پہلے پہل ہندسوں کے ذریعے ہی ریاضی کی بنیاد ڈالی۔ انھوں نے ہندسوں سے متعلق بڑے منطقی اور فلسفیانہ قصے منسوب کررکھے تھے۔ اسی لئے ہندسوں کی یہ دنیا بڑی دلچسپ اور سحرانگیز ہے۔ 

ہر ایک ہندسہ اپنے اندر مخصوص خوبیاں سمیٹے ہوئے ہے۔ مثلاً صفر ایک ایسا ہندسہ ہے جو سب ہندسوں کے آخر میں دریافت ہوا لیکن ریاضی کا سب سے اہم اور ضروری عدد بن گیا۔ اس کی قیمت کچھ بھی نہیں ہوتی لیکن دوسرے اعداد کے ساتھ ملانے پر وہ بڑی بڑی رقمیں بن جاتی ہیں۔ ریاضی کا پہلا ہندسہ ایک (1) ہے اور دیگر تعداد یا اعداد کو سمجھنے میں مدد دیتا ہے۔ عدد چار( 4) پہلا پرفیکٹ اسکوائر یعنی 2(2) ہے۔تین ایک طاق عدد ہےحتی کہ یہ سلسلہ نو(9) تک پہنچتا ہےجوکہ سب سے بڑا ہندسہ ہے۔ریاضی میں فرض اعداد کا تصور بھی موجود ہے۔ 

مثلاً منفی ایک( 1-) ،منفی دو( 2-)،منفی تین( 3-) وغیرہ ان کی حیثیت ان کے مساوی مثبت اعداد سے ایسی ہوتی ہے، جیسے طبیعیات میں مادّہ اور ضدمادّہ کی ہوتی ہے کہ اگر کہیں مادّہ اور ضدمادہ آپس میں مل جائیں تو وہ ایک دوسرے کو فنا کردیں گے اور نتیجتاً کچھ بھی نہیں بچے گا۔ایسےہی 1+ کو 1- سے ملایا جائے تو آخر میں "0" یعنی کچھ بھی نہیں بچے گا۔ 

اعداد کی خصوصیات کو سمجھنے کے لئے ریاضی میں ایک الگ ہی شاخ ہے جسے نمبر تھیوری (Number Theory) کہتے ہیں۔اس کے علاوہ الجبرا، میٹرکس(Metrix)، اینالٹک جیومیٹری( Analytic Geometry) ویکٹرز وغیرہ اور ٹوپولوجی( Topology) ریارضی کی سب سے جدید ترین شاخ ہے، جس میں ہر قسم کے ’’فاصلے‘‘ (Space) کی ہیئت، ساخت اور خصوصیات کا مطالعہ کیا جاتا ہے۔ مشہور فلسفی و ریاضی دان فیثاغورث کا کہنا تھا کہ ’’کائنات کی تشریح صرف ہندسوں کے ذریعے ہی ممکن ہے، کیوں کہ مظاہر فطرت و قدرت کی زبان صرف ریاضی ہے‘‘۔